
About 2.m √ (q +1) (mm)ī l = Length of worm wheel. Note: for α n= 20 o γ should be less than 25 oī a = Effective face width of worm wheel. Α n = Normal pressure angle = 20 o as standard Of the gear shows that, at this plane, the meshing teeth and thread section is similar Other alignments are used less frequently.Īs can be seen in the above view a section through the axis of the worm and the centre The gearset can also be arranged with the The worm is shown with the worm above the wormwheel. However this option has the highest load capacity, near zero backlash capability, highest accuracy and extended life capability.Ī more detailed view showing a cylinderical worm and an enveloping gear. The double enveloping (double throat/double globoid ) option is the most difficult to manufacture and Double enveloping gearsets require accurateĪlignment of both the worm and the wormwheel to obtain maximum face contact.ĭiagram showing the different worm gear options available.
GEAR DESIGN PARAMETERS FULL
The worm-wheel to ensure full line tooth contact. Single enveloping gearsets require accurate alignment of If the worm is machined withĪ concave profile to effectively wrap around the wormwheel the gearset is called a double enveloping worm gearsetĪnd has the highest power capacity for the size. This is called a single envelope worm gearset. However normally the wormwheel is cut with a concave as opposed to a straight If the worm gears are machined basically as crossed helical gears the result is a highly stress The size of the worm gearset is generally based on theĬentre distance between the worm and the wormwheel. The worm is similar to a screw and the worm wheel is similar to a section of a nut.Īs the worm is rotated the wormwheel is caused to rotate due to the screw like action Worm wheel with a worm screw meshing with teeth on the periphery of the worm wheel. A worm drive consists of a large diameter A basic helical gear can be used but the power It is recommended that you replace the calculated real value with an integer value.Ĭheck the Gear 2 box to enter values for Gear 2.A worm gear is used when a large speed reduction ratio is required betweenĬrossed axis shafts which do not intersect. Select to calculate the helix angle according to the center distance and other input parameters. Select to calculate the unit summary correction according to the center distance and other input parameters. Options are enabled if you select Module and Number of Teeth option from the drop-down list in the Common area. Typically, select this option if using English units. Typically, select this option if using metric units. Select to calculate the gear ratio according to number of teeth. Select to calculate number of teeth of the second gear according to gear ratio. To display the More Options area, click More in the right lower corner of the Design Tab. If not available, calculate total unit correction based on other parameters.Ĭlick to display the Preview dialog box with a schematic image of spur gears dimensions.ĭisplays additional options for spur gear design.
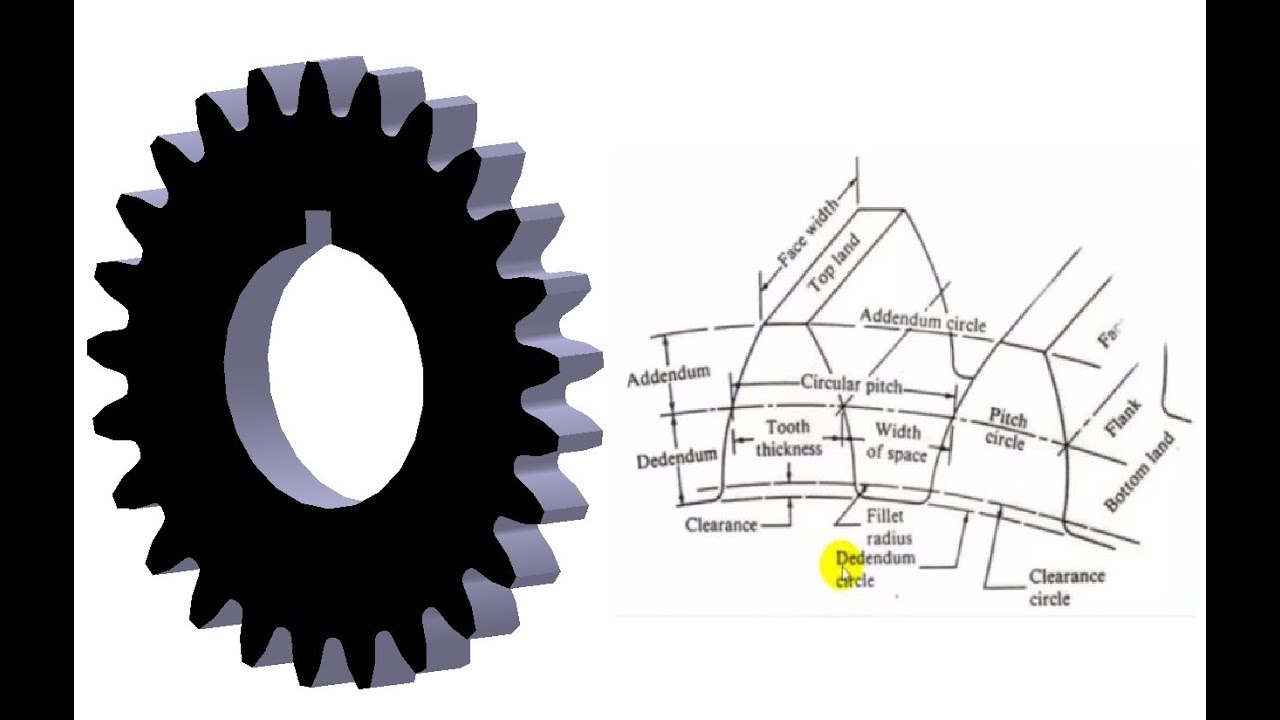
Not available if you select Total Unit Correction option in the Design Guide drop-down menu. Specifies the sum of the gear unit corrections. Specifies the method to use for calculation of the teeth correction. to change direction you must click Flip next to the edit field. You can insert only positive values from 0 to 55. Helix angle is the angle that a helical gear tooth makes with the gear axis at the pitch circle. In involute teeth, the pressure angle is often described as the angle between the line of action and the line tangent to the pitch circled. Pressure angle is the angle between a tooth profile and a radial line at its pitch point. This option is disabled when you select Center Distance in the Design Guide drop-down menu - you want to calculate center distance based on other input parameters. Specifies the shortest distance between centers of gears. Note: This option is enabled if you select Diametral Pitch in the Size Type area of More options.


 0 kommentar(er)
0 kommentar(er)
